1. Bevezetés

 

A hangról általában mindenki tudja, hogy rugalmas közegben terjedő mechanikai hullám, de az ultrahanggal kapcsolatban hazai interdiszciplináris konferencián még ma is felmerül olyan kérdés, hogy -ha rákiabálunk egy sejtre, az attól valóban képes megváltoztatni az aktivitását-? A meglepő válasz az, hogy igen! Ez pontosan így történhet abban az esetben, ha elég hangosak vagyunk. Azonban egy ágyú elsütésekor az ágyúcső nyílása mellett közvetlenül 0,001W/cm² hangenergia mérhető, ugyanakkor mi pedig általában 10W/cm², vagy e feletti teljesítményekkel dolgozunk az anyagban, 1MHz körüli frekvenciatartományokban. Ez tehát akkora intenzitás, mintha a fülünk mellett közvetlenül egyszerre 10000 ágyút sütnének el. Így már könnyebb elképzelni, hogy ez biológiailag, illetve fizikailag mennyire hatékony lehet.

Ez az iszonyatosan nagy hangenergia „bűvös” dolgokra képes. Különböző akusztikai jelenségek alakulhatnak ki általa az anyagban, melyek egy részét ma már jól ismerjük, természetesnek tartjuk és alkalmazzuk, míg mások napjainkban kerülnek a tudomány homlokterébe. Néhány ilyen ismert akusztikai jelenség a kavitáció, az akusztikai áramlás, az állóhullám, a szökőkút-jelenség, az atomizáció, a szonolumineszcencia és a hőhatás.

Gyakran azt tapasztalom, hogy az ultrahang közvetlen alkalmazói nem tudják, hogy micsoda szenzációs eszköz van kezükben, céljaik megvalósítására, illetve a tudományos látókörük további kiszélesítésére. Sajnos nagyon sokszor az is előfordul, főleg ahol egy folyamat részeként használják az ultrahangot, tehát ahol természetesen nem a célja, hanem az eszköze egy technológiai sornak, vagy egy kutatásnak (sejt anyagcseretermékek kinyerésénél preparatív munka előkészítésekor, vagy az analitikai eluensek gáztalanításánál), hogy hatékonyságbeli problémákat okoz a szakszerűtlen alkalmazás, melyet egyszerű szakfogásokkal és „trükkökkel” orvosolni lehet.

Az elkövetkezendőkben ezeket a trükköket, szakfogásokat tárgyalom, az ultrahang konvencionális és a legmodernebb felhasználási lehetőségeinek tükrében, remélhetőleg mindenki számára izgalmas példákkal, saját kutatási tapasztalataim alapján.

 

2. UltrahangFizikai alapok

2.1. Hullámtan

 

Az ultrahang 16kHz frekvencia feletti mechanikai hullámokat jelent. Természetesen ez a frekvenciatartomány már az emberi fül számára általában már hallhatatlan, de nem úgy a kutyák, vagy például a denevérek számára, melyek a 30-50kHz-es frekvenciatartományt is kiválóan érzékelik.

Az ultrahangot aktív és passzív tartományra oszthatjuk, vagyis megállapodás szerint az 1W/cm² vagyis a 10000W/m² teljesítmény alatt passzív, míg felette aktív ultrahangról beszélünk. A passzív ultrahangot leginkább az anyagtulajdonságok vizsgálatára, míg az aktív ultrahangot az anyag tulajdonságainak a megváltoztatására alkalmazzuk.

Az aktív ultrahang anyagtulajdonság befolyásoló képessége az anyagban kialakuló hullám- és akusztikai jelenségekkel függ össze. Folyadékokban és gázokban longitudinális hullámok, míg szilárd anyagokban emellett többek között a tranzverzális és a tágulási hullámok is jellemzőek, melyekre többek között egy adott szilárd anyagban eltérő hangsebességek jellemzőek. Longitudinális hullám esetén a hullámmozgást végző közeg sűrűsödései (C) és ritkulásai (R) a hullám terjedésének irányában vannak (1. ábra).

 

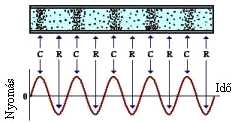
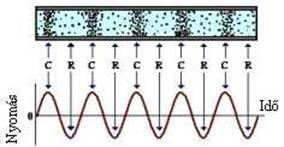
1. Ábra: Longitudinális hullám (C, sűrűsödések, R, ritkulások)

 

Mivel a legtöbb aktív ultrahang alkalmazást (kivéve például az ultrahanghegesztés és forrasztás) a folyadékokra és a folyadékszerű anyagokra alkalmazzuk, ezért e tanulmányban a folyadékközegekre jellemző hullám-, és akusztikai jelenségekkel és azok alkalmazásával foglalkozom.

A longitudinális hullámoknál, amennyiben egy szinusz hullámra gondolunk (2. ábra), úgy rögtön szemünk előtt lebeg, hogy egy hullámon belül van egy fel- és egy lefelé irányuló ív, ami együttesen egy hullámhossz (λ) nagyságú, amely az adott anyagra jellemző hangterjedés sebességének (c) és az alkalmazott frekvenciának (f) a hányadosa, vagyis λ=c/f.

 

2. Ábra: Szinusz hullám

 

A szinusz hullámban az ívek vízszintes középtengelytől számított magassága és mélysége az amplitúdó. A hullámhossz többek között abban is alapvető szerepet játszik, hogy mennyire irányítható a hangsugár. A téma jelentőségére történelmi példát idézek. Horthy Miklós korai „csillagháborús” törekvései a múlt században, jellegükből fakadóan természetesen érintették az ultrahangot is, mint az akkori egyik legtöbbet ígérő provizórikus technikát. Ez a lendület Békésy György, 1961-ben orvosi Nobel-díjat kapott Professzor magyarázatára szerencsére alábbhagyott, miszerint az ultrahangot fegyverként alkalmazni, célszerűen valamely távoli objektum irányított elpusztítása céljából lehetetlen, mivel kizárólag a magas frekvencián irányítható jól a hang, illetve az a hullámhossz-csökkenésével (frekvencia növekedésével) egyenes arányban növekvő mértékben adszorbeálódik a levegőben, illetve bármely közegben. Az előző példával tehát azt próbáltam érzékeltetni, hogy milyen fontos összefüggésben van a hullámhossz, a frekvencia és a kezelt anyag minősége.

Magától értetődő módon, azonos anyagban kisebb távokon a hangok elnyelődése, abszorpciója kisebb mértékű, tehát az irányított, linearizált hangsugárral nagyon komoly tevékenységeket lehet folytatni. Szép példa erre mentorom, Greguss Pál Professzor tevékenysége, aki az akusztikus holográfia nemzetközileg elismert megalkotója és az 1971–ben (a holográfia linearizált fény, vagyis a lézer segítségével történő megvalósításáért) fizikai Nobel-díjat kapott Gábor Dénes pálya- és versenytársa, illetve a PAL (Panoramic Annular Lens) optika feltalálója volt. Hasonló jelenség érhető el tehát mechanikai, vagyis hanghullámokkal, mint elektromágneses hullámokkal, vagyis előállítható hologram ultrahang segítségével is, nem csak lézerrel.

Az irányított, linearizált hangsugár alkalmazására további szinte sci-fi regényekbe illő példa a már hazánkban is nagy sikerrel alkalmazott, az egészségbiztosítási pénztár által 2004. január 1.-től támogatott MR-re (Mágneses Magrezonanca) alapozott vágás nélküli ultrahang sebészeti eljárás, hangsugarak segítségével, ahol ambuláns módon, nem kísérletileg, hanem alkalmazott eljárásként történik a daganatok eltávolítása. Más szóval az operáció egyetlen vágás nélkül elvégezhető úgy, hogy a beavatkozás után rögtön távozhat a beteg, és a műtét nem befolyásolja negatívan a páciens életminőségét és munkaképességét. Magyarországon alkalmazott, nem kísérleti jellegű eljárásról van szó! Világszinten, a fókuszált ultrahangos sebészeti eljárást egyre gyakrabban alkalmazzák, -igaz ma még kísérletileg- a koponya felnyitása nélküli agydaganat eltávolítására is. A technológia jelenleg a 0,1mm pontossági határon tart, amely már az emberi kéz pozicionálási képességén is túlmutat.

 

2.1.1. A hangsugár elváltozásai a hangtérben

 

A longitudinális hanghullám akusztikai határfelülethez érve, vagyis a hangvezető közegtől eltérő akusztikai keménységű közegnél reflektálódik, elhajlik, törik, illetve bizonyos esetekben szóródik (3. ábra). A hangszóródás tehát ott jelentkezik, ahol a hullámok rugalmas közegbe ágyazott idegen testhez, akadályhoz érnek. A reflexiós és az átbocsátási fok meghatározására általában a következő [1-3]. képletet alkalmazzuk Tarnóczy (1963) szerint, a folyadékba merülő, folyadéktól eltérő akusztikai keménységű lemezre, illetve idegen testre vonatkozóan:

 

R=((q²-1)²)/((q²+1)²+4q²ctg²(2πd/λ))         [1].

q=(ρ₂*c₂)/(ρ₁*c₁)                                         [2].

z= ρ*c                                                           [3].

 

Ahol (R) a visszaverődési fok, (z) az akusztikai keménység, (q) a két közeg akusztikai keménységének hányadosa, (d) a lemez (test) vastagsága, (λ) a lemezben (testben) kialakuló hullámhossz, (ρ) a térfogattömeg, (c) a hangsebesség adott közegben.

Az [1]. képlet lényege, hogy z=ρ₁*c₁ akusztikai keménységű közegbe ρ₂*c₂ akusztikai keménységű (d) vastagságú lemez, illetve test merül. Ekkor a lemezre merőlegesen beeső hangrezgések visszaverődési foka: (R). Ebből az átvezetési fok: S=1-R.

 

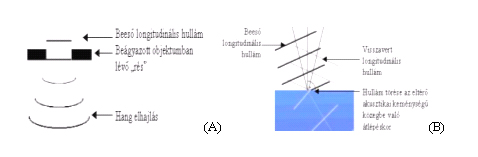
3. Ábra: A longitudinális hullámok alapvető elváltozásai (A, hullám elhajlás, B, törés, reflexió)

 

A hullámok viselkedésének megértéséhez alapvető szempont az akusztikai keménység figyelembe vétele. A 3.A. ábrán megfigyelhető, hogy az eredeti hangvezető közegbe ágyazott eltérő akusztikai keménységű térelemen lévő résen a longitudinális hullámok elhajlanak, illetve a hullámhosszhoz viszonyítva megfelelően kis rés esetében gömbhullámok alakulnak ki.

A 3.B. ábrán megfigyelhető, hogy az akusztikailag lágyabb közeg felől történő hullám belépéskor (például levegőből vízbe lépéskor) a hullámok törnek és reflektálódnak, illetve egy bizonyos belépési szög alatt az összes beeső hullám reflektálódik és semmi nem lép be a folyadékba. Az akusztikai keménység (z) tehát a közeg sűrűségének (ρ) és hangvezetési sebességnek (c) a szorzata, vagyis z=c*ρ. Könnyűszerrel belátható, hogy amennyiben egy vízben terjedő longitudinális hanghullám például gáznemű közeg határához ér, akkor a közel négy nagyságrendnyi akusztikai keménység különbség miatt majdnem 100%-ban visszaverődik onnan.

 

2.1.2. Az álló- és a haladó hullámok kialakulásának fizikai alapjai

 

A hullámok találkozásánál a visszaverődés miatt interferencia lép fel, mely a hullámpontok helyi és pillanatnyi értékeinek előjel és nagyság szerinti összegződése, amelyekből egy eredő hullám alakul ki, a találkozó hullámok szuperpozíciójaként. Akkor alakul ki állóhullám, ha két azonos típusú, frekvenciájú és amplitúdójú, de ellentétes irányú hullám találkozik, tehát az állóhullám interferencia jelenség. Nagyon fontos, hogy az állóhullám olyan hullám, melynek mentén a csomópontok és duzzadó helyek térbeli elhelyezkedése nem változik (4. ábra).

Érdekes az a tény, hogy amennyiben folyadékfelületről történik a hullám visszaverődése, akkor a sebességi csomópontokban (a hullám maximális sebességi pontjai), amikor szilárd felületről történik a reflexió, akkor a nyomási csomópontokban (a hullám maximális nyomási pontjai) történik meg a maximális akusztikai nyomás amplitúdójú visszaverődés. Minden más hullámpont általi reflexiós felület érintés a beeső hullámhoz képest gyengített visszavert hullámot eredményez. Persze ellenkező esetben, ha a folyadékfelületről a nyomási és a szilárd felületről a sebességi csomópontban történik határfelület érintés, akkor kioltásról beszélünk, tehát nincs visszaverődés és nincs állóhullám sem. Ehhez a gyengítési hatáshoz járulhat még hozzá a közegek közötti eltérő akusztikai keménység érték, valamint a beesési szög, amelyek alapján dől el, hogy az eredeti hullám energiájának mekkora része hatol be egy anyagba.

Hogy a reflexiós felületet érintő hullámpont jelentőségét érzékeltetni tudjam, nézzünk meg egy szinusz hullámot, mely vízben halad és 1MHz frekvenciájú. Ennek a hullámnak a hullámhossza λ=c/f összefüggés szerint λ=1482(m/s)/1000000(1/s)=1,48mm. Ez azt jelenti, hogy 1,48mm-en belül 2 helyen, vagyis 0,74mm-en dől el, hogy maximális reflexiós hatást kapok-e és fel tud-e épülni az állóhullám, vagy kioltást eredményez a reflexió, tehát 0,74mm-en belül alakul ki a „mindent, vagy semmit” hatás.

 

4. Ábra: Állóhullám séma

 

Az állóhullám tehát általában úgy keletkezik, hogy egy haladó hullám valamilyen akadályon, például levegő határfelületen visszaverődik és az eredeti, valamint a visszavert hullám interferál.

Ha egy irányba halad a hullám, akkor haladó hullámról van szó. Ebben az esetben a longitudinális hullámot a legegyszerűbben a 2. ábrán ábrázolt szinusz hullámok hosszú soraként képzeljük el a térben, melyek amplitúdója, azaz az íveik magassága és mélysége a sugárzótól távolodva egyre kisebb, vagyis a hangintenzitás így csökken az adszorpció miatt. (Természetesen más hullámformák is elképzelhetőek, így négyszög, háromszög, stb.) A Huygens-elv kimondja, hogy a közeg minden egyes pontja az odaérkező hullám hatására pontszerű gömbi hullámforrássá változik, azaz a hullámfront minden pontja újabb hullámforrás, amelyből további hullámok indulnak ki.

A hullámhosszhoz viszonyított nagyon kicsi részecskék képesek együtt mozogni a térrel, illetve arról gömb hullámok terjednek tova, amelyek a vezető hullámok energiájának egy részét elvonják, adszorbeálják, szétszórják, diszpergálják a térben.

 

 

 

2.1.3. Near field – Far field

 

Az ultrahangtérben a hangnyalábot feloszthatjuk hektikus energia eloszlású közeltérre (near-field), illetve egyenletesebb energia eloszlású távoltérre (far-field) (5. ábra).

 

 

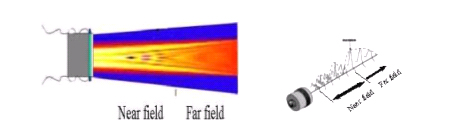
5. Ábra: A közel- és távoltér elhelyezkedése a sugárzás irányában

 

A közel-, és távoltér határa kör alakú rezonátorra N_kör=d²*f/4*c, amely képletben a (d) a rezgő átmérője, az (f) a frekvencia, a (c) pedig a hangsebesség. A hangtér tehát a tér minden olyan pontja, ahol a hanghullámokra jellemző, váltakozó nyomás lép fel. A közel és távolteret a tudomány és az alkalmazott technika eltérően ítéli meg. Abban az esetben, ha kavitációs technikát alkalmazunk (tisztítás, sejtroncsolás, stb.), teljesen mindegy, hogy mely zónában dolgozunk, mivel az amplitúdót a kavitációs szint fölé emelve drasztikus hatás érvényesül a hangtér minden egyes pontján. Azonban irányított, vagy finom kísérleteket és technikákat általában ajánlott a távol térben végezni, mivel itt az előzőekben is említett módon sokkal kiszámíthatóbb, tervezhetőbb az akusztikai energia eloszlása. Az 5. ábrán megfigyelhetőek az úgynevezett gyengítési interferenciazónák, melyek a közel térben lévő hidegebb színnel jelölt területek, és ami miatt hektikusabb a közel tér energia eloszlása. Ezek a területek a sugárzás jellegéből fakadóan alakulnak ki, kiküszöbölésükre vagy fázisgyűrűs koncentrátorokat, vagy a későbbiekben említett kompozit-kerámiákat alkalmazhatjuk.

 

2.1.4. Levitáció

 

Az előzőekben tehát tisztáztuk az álló és a haladó hullámok fogalmát, illetve azt, hogy az akusztikai állóhullámtérben a hullámhosszhoz viszonyított kis méretű részecskék képesek a hanghullámmal együtt mozogni, azaz akár folyadékban, akár gáznemű közegekben képes kialakulni a levitáció, vagyis a tárgyak, fizikai objektumok lebegése (6. ábra).

 

 

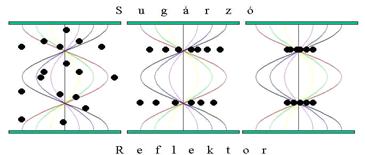
6. Ábra: Az állóhullám részecskekoncentrációs hatása

 

A 6. ábra azt mutatja, hogy az akusztikai állóhullámtérben a hullámhossznál kisebb részecskék hogyan rendeződnek el az állóhullám időbeli jelenlétének előrehaladtával.

Abban az esetben, ha a vivőközegnél nagyobb sűrűségű szemcséket diszpergálunk a térben, akkor a nyomási, ellenkező esetben a sebességi csomósíkokba rendeződnek. E jelenséget először Kundt mutatta be látványosan a „Kundt cső” segítségével a XIX. század végén. E zseniális fizikai jelenségre napjainkban egyre-másra születnek a futurisztikus alkalmazások, amelyről elöljáróban talán elég annyit elmondani, hogy jelenleg a NASA-nak ez az egyik legkomolyabban támogatott programja. Ezáltal a földön kialakítható az anti- vagy mikrogravitációs tér, vagyis kvázi űrkörülményeket teremthetünk itt a földön (7. ábra), amivel rengeteg pénzt és kockázatot spórolnak a költséges űrkísérleteken. A 8. ábra akusztikai levitátor sémát mutat.

 

 

7. Ábra: Akusztikai levitáció (A, lebegő habpamacsok (SAAL technika), B, lebegő olvadt fém TAAL technika, C, lebegő folyadékcseppek (SAAL technika))

 

 

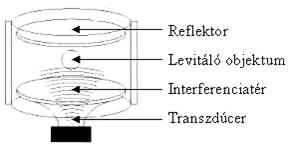
8. Ábra: Akusztikai levitátor séma

 

A SAAL technika az egy akusztikai tengelyre (Single Axis Acoustical Levitator), a TAAL technika pedig a három akusztikai tengelyű (Three Axis Acoustical Levitator) eljárásra utal. Természetesen az alkalmazások közt az dönt, hogy milyen fajsúlyú, milyen minőségű, mekkora mennyiségű minta lebegtetését akarjuk megoldani. A 7.B. ábra éppen lebegtetett fém szemcsét mutat be, melyet lézer segítségével megolvasztanak és ezután vagy spektrometriai, vagy egyéb típusú analitikai vizsgálatokat tudnak elvégezni azon. A SAAL technikák érthető okokból, az alacsonyabb akusztikai nyomás amplitúdó (kisebb akusztikai térintenzitás) miatt inkább a kisebb fajsúlyú szemcsék, lapkák, pászmák cseppek lebegtetésére alkalmasak. A másik ok az egy, illetve a háromtengelyű alkalmazásra a lebegő csepp alakja. Mivel ha elképzelünk egy álló szinusz hullámot (4., 6., ábra), akkor könnyű belátni, hogy egy tengely esetén a csepp formája diszkosz, kettő esetén szivar, három esetén viszont gömb formájúra módosul. Persze egy tengely esetén is vannak alkalmazási módok a kvázi gömb alakú lebegő objektum kialakítására, azonban a TAAL technika kiszélesíti a skáláját a vizsgálható objektumoknak.

Magától értetődő módon ennél az alkalmazásnál elsősorban nem arról van szó, hogy egy embert, vagy egy űrhajót akarnak lebegtetni a földfelszín felett, aki a rakétában kísérletezik, hanem azokat a fizikai, kémiai és biológiai kísérleteket szeretnék a földön olcsóbban elvégezni, melyekből, ha eddig összejött 20-30db, akkor azért már fellőttek egy űrhajót. Soha nem látott lehetőségek adódtak ezzel a kristályosítás, szövettenyésztés, sejt anyagcseretermékek kialakítása, új biokémiai reakció utak, sejt- és telepmorfológiai formák és rengeteg egyéb például fém analitikai alkalmazásokra. Ismét csak emlékeztetni szeretnék minden kedves olvasót, hogy ne felejtsük el, hogy ez egy vadonatúj, általunk is alkalmazható technika.

Ha sikerült e hazánkban és világszerte még teljes mértékben kiaknázatlan technológia iránt érdeklődést indukálnom, úgy keressék a kontaktust, a szükséges technikai feltételek kialakításáért, mivel sorozatgyártású levitátor még 2003 első félévéig nem jelent meg a piacon, az eltérő tudományos igények miatt.

 

2.2. Nemlineáris akusztikai jelenségek, akusztikai áramlás

 

Fontos megemlíteni az akusztikai áramlást, mely a folyadék nemlineáris viselkedése következtében alakul ki, mivel a folyadék kevésbé összenyomható, mint amennyire kitágul, illetve azért, mert a térben nem egységes az energia disszipáció. Az áramlást két nemlineáris jelenség alakítja ki, melyek közül az egyik a folyadék dinamikájának nemlineáris viselkedése, ami a tehetetlenségi erő dominanciáját jelenti a viszkozitási erővel szemben, a másik a nemlineáris akusztikai hatás, ami az akusztikai áramlás hajtóerejének alapja. Képletesen gondoljunk egy tengeri hullámra, amely tornyosul, majd önmagán átbukik a véges amplitúdók miatt (9. ábra).

 

 

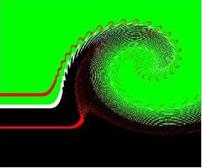
9. Ábra: Felületi hullám torzulása

 

A fenti ábrához hasonlóan torzul a szinusz hullám is a térbeli haladása közben (10. ábra), méghozzá a hullám pozitív részében egyre nagyobb amplitúdó értékek alakulnak ki a transzdúcertől távolodva, illetve közelebb jár a valósághoz, ha inkább lökéshullám (Shock Wave) kialakulásról beszélünk, persze azon a hullám által megtett úton, amelyen még nem adszorbeálódik és alakul hővé a hullám energiája.

 

 

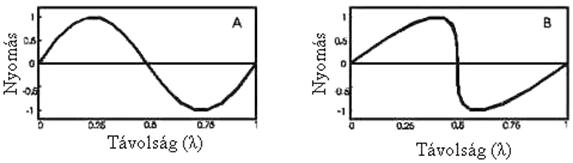
10. Ábra: A szinusz hullám (A) és torzulása (lökéshullám) (B)

Tipikusan nemlineáris jelenség akusztikai áramlás, vagy „kvarcszél” amely egy állandó folyadékmozgás, amit az intenzív ultrahang okoz a fent vázolt fizikai okok miatt. Ennek során a folyadékban szemmel látható keveredés, turbulencia tapasztalható, amelynek látványos élményszerűsége csak fokozható indikátoranyagok (festékek) folyadékhoz adagolásával (11. ábra). Félretéve a viccet, az akusztikai keverőhatás akár az élelmiszer-, akár a vegyipar, bio-, és környezettechnika számára tartogat újdonságokat, ugyanis a keverés mellett „egy menetben” megvalósítható a diszpergálás (emulzió és szuszpenzió előállítás), a csírák serkentése, vagy éppen gátlása, roncsolása. Természetesen a technológia alkalmazhatóságának néhány esetben határt szabhatnak a kezelendő anyag fizikai tulajdonságai, pontosabban inkább az extrém körülményekhez szükséges berendezések kialakításának költségei. Szélsőséges, de az 1960-as években megoldott esetnek számít, az ultrahangos bitumen keverési eljárás aerodinamikus ultrahang generátor segítségével. A legtöbb folyadék esetében akár önállóan, akár kombinált eljárásként, az előbb felsorolt műveletek elősegítésére, vagy a hő-, és anyagtranszport folyamatok intenzívebbé tételére alkalmazható az ultrahang.

 

 

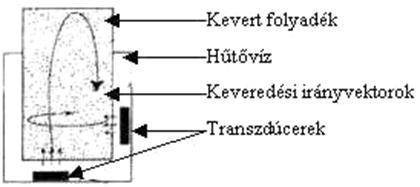
11. Ábra: Ultrahangos folyadékkeverő

 

Az ultrahang története során többször felmerült a lökéshullám jelenség vagy az akusztikai nyomás amplitúdó nagyság miatt, hogy mivel az akusztikai nyomás amplitúdó növekedése, vagyis a hullámtorzulás (9., 10. ábra) kis kibocsátott ultrahang intenzitások mellett is előfordul, akkor mi a helyzet a diagnosztikai ultrahanggal? Köztudott, hogy a diagnosztikai ultrahangot például a folyadékkal telt, vagy a savós testüregek feltérképezésére, így például a magzatnak a magzatvízen, a szívnek a véren, vesének a vizeleten keresztül való vizsgálatához alkalmazzák többek között. Az 1970’-es években az egyre erősödő tudományos nyomásra hirtelen „felfedezték” hogy ez a hullámtorzulás bizony ezeken a helyeken is kialakul, ami nem lenne baj, mert képen modellezve ez nagyon látványos jelenség (9. ábra), csakhogy a növekvő akusztikai nyomás amplitúdó (a lökéshullám) az ultrahang egyik legdrasztikusabb későbbiekben tárgyalt akusztikai jelenségét, a kavitációt váltja ki ezeken a helyeken is. A kavitáció pedig nemcsak a sejtek, makromolekulák, de még a legkeményebb fémek szétroncsolásának is az alapvető akusztikai kiváltója. Emiatt a 70’-es évek végén 80’-as évek elején pánikszerűen kijelölték a legmagasabb intenzitást, amelyet a diagnosztikai ultrahangnál alkalmazni lehet, vagyis azt az intenzitást, amely elméletileg a reflexióhoz elegendő csak és a szövetekben „gyorsan” adszorbeálódik, különösebb hőképződés nélkül. Búvópatakként, természetesen újra és újra előkerül a téma a konkurens technológiák bevezetésénél, amire például, az ECMUS, BMUS, WFUMB szervezetek majdnem évente kiadnak egy aktuális biztonsági szintet, természetesen külön az egyes diagnosztikai alkalmazásokra és berendezés típusokra. Végső soron leszögezhető azonban, hogy a diagnosztikai ultrahang maximális intenzitása 1W/cm² alatt néhány száz mW/cm² körüli érték (már évek óta).

 

2.2.1. Atomizáció

 

Az akusztikai áramlás, illetve a hullámtorzulás átviteles, járulékos hatása az atomizáció. Ez a jelenség, az ultrahanggal besugárzott folyadékok (víz, fertőtlenítőszer, olvadt fémek, stb.) kiporlasztását jelenti, amelynek kapcsán „szökőkút” jelenség is kialakul, ami szintén egy igen látványos, azonban például az asztmakezelésben és rakéta és járműipari technikában annál hasznosabb jelenség (12. ábra).

Az atomizáció kapcsán a folyadékszemcsék a gázközegbe kerülnek, mely folyadékrészecskék hordozhatnak fertőtlenítő- és gyógy- és növényvédő szert, bevonó, festék- és üzemanyagot, stb. Érdekes jelenség alakul ki, amikor eltérő sűrűségű, egymással nem elegyedő folyadékok helyezkednek el egymás felett, és alulról történik az ultrahang besugárzás. Ekkor az alsó nehezebb közeg felé alakul ki ez a „szökőkút” alakzat és nincsen kiporlasztás sem.

 

 

12. Ábra: Ultrahangos atomizáció (A, akusztikus inhaláló, B, szökőkút jelenség és atomizáció (Forrás: Lőrincz, A., 2003), C, akusztikus porlasztó)